Есть несколько способов найти площадь неправильного четырехугольника.
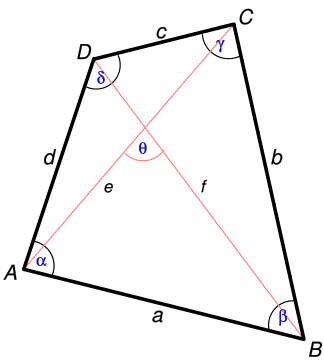https://en.wikipedia.org/wiki/File:Tetragon_measures.svg
Картинка: википедия
- Вы знаете длины диагоналей и размер угла между ними. Тогда площадь четырехугольника можно найти по формуле
Калькулятор:
Содержание
Площадь выпуклого четырехугольника
Диагональ 1 Диагональ 2 Угол между диагоналями ° ′ ″ Точность вычисленияЗнаков после запятой: 2 Рассчитать Площадь content_copy Ссылка save Сохранить extension Виджет
- Вы знаете длины четырех сторон и размеры двух противолежащих углов. Тогда площадь четырехугольника можно найти по формуле Бретшнайдера.
,
где s — полупериметр.
Калькулятор:
Площадь четырехугольника по четырем сторонам и двум противолежащим углам
Сторона a Сторона b Сторона c Сторона d Угол alpha ° ′ ″ Угол gamma ° ′ ″ Точность вычисленияЗнаков после запятой: 2 Рассчитать Площадь content_copy Ссылка save Сохранить extension Виджет
- Вы знаете длины четырех сторон и длины диагоналей. Тогда площадь четырехугольника тоже можно найти по формуле Бретшнайдера.
,
где s — полупериметр
Калькулятор:
Площадь четырехугольника по четырем сторонам и двум диагоналям
Сторона a Сторона b Сторона c Сторона d Диагональ e Диагональ f Точность вычисленияЗнаков после запятой: 2 Рассчитать Площадь content_copy Ссылка save Сохранить extension Виджет
- Вы знаете длины четырех сторон и то, что четырехугольник является вписанным в окружность. Тогда вы имеете дело с частным случаем формулы Бретшнайдера (сумма двух противолежащих углов известна и равна 180), известным как формула Брахмагупты.
,
где s — полупериметр
Для вычисления можно использовать калькулятор выше, введя произвольно два угла так, чтобы их сумма составляла 180.
Вывод самих формул Бретшнайдера можно посмотреть .
Ну и напоследок еще раз упомяну, что зная только длины четырех сторон вычислить площадь четырехугольника нельзя, так как нельзя однозначно определить его вид — нужно еще какое-нибудь ограничивающее условие. Так как у нас на сайте довольно часто просили посчитать площадь четырехугольника только по четырем сторонам, то еще есть вот такой вот шуточный калькулятор: Площадь неправильного четырехугольника с заданными сторонами, который бесконечно рассчитывает такие площади.
Четырехугольником называется фигура, состоящая из четырех вершин, три из которых не лежат на одной прямой, и отрезков, соединяющих их.
Существует множество четырехугольников. К ним относятся параллелограммы, квадраты, ромбы, трапеции. Найти площадь квадрата можно найти по сторонам, площадь ромба легко вычисляется по диагоналям. В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Для начала рассмотрим формулу площади четырехугольника через диагональ. Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними. Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле:
Половина произведения диагоналей и синуса острого угла между ними является площадью четырехугольника. Рассмотрим пример расчета площади четырехугольника через диагональ.
Пусть дан четырехугольник с двумя диагоналями d1=5 см;d2=4см. Острый угол между ними равен α = 30°. Формула площади четырехугольника через диагонали легко применяется для известных условий. Подставим данные:
На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет площади параллелограмма.
Площадь четырехугольника по сторонам
Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так: 
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:
Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a = 5 см, b = 4 см, с = 3 см, d = 6 см. Для начала найдем полупериметр:
используем найденное значение для расчета площади:
Площадь четырехугольника, заданного координатами
Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.
Дан квадрат ABCD, расположенный в системе координат XY. Найти площадь фигуры, если координаты вершин A(2;10); B(10;8); C(8;0); D(0;2).
Мы знаем, что все стороны фигуры равны, и формула площади квадрата находится по формуле:
Найдем одну из сторон, к примеру, AB:
Подставим значения в формулу:
Знаем, что все стороны одинаковые. Подставляем значение в формулу расчета площади: