Площадь участка по координатам

Что такое план статьи и как его правильно составить: советы и примеры

Привет всем, кто решил познавать искусство письма! С вами Анна – копирайтер с двухлетним стажем, написавший более 500 статей. Сегодня у нас важный урок.

Думаю, вам не раз встречались тексты в интернете, в которых сложно уловить суть. Автор резко переходит от одной мысли к другой, отходит от темы. Хочется закрыть этот кошмар и забыть о нем.

Чтобы вы избежали участи горе-писателя, работы которого никому не нужны, я вам покажу, как составить план текста просто и правильно, также объясню, что это такое.

Пользуйтесь моими советами, чтобы подняться на новый уровень в копирайтинге.

Что такое план текста и зачем он нужен?

План статьи – это список, состоящий из основных мыслей статьи, которые изложены в логической последовательности. Главная задача – раскрыть содержание. Идеальной структурой считается та, при взгляде на которую вспоминается весь текст.

Каждый пункт списка – ориентир, помогающий понять суть статьи.

Зачем копирайтеру составлять и продумывать план:

• избавиться от каши в голове, разложить всю информацию по полочкам;
• сделать материал полезным, увлекательным для читателя;
• благодаря продуманной структуре, читатель легко найдет нужный ему блок информации;
• количество клиентов, восторженных отзывов вырастет вместе с вашим доходом.

Умение структурировать помогает готовиться к экзаменам, анализировать статьи конкурентов.

Составляем структуру правильно: подробная инструкция

Когда первый раз садишься писать план, обычно в голове начинается хаос, сложно выделить основную мысль. В итоге пункты, которые должны быть короткими, раздуваются до целых абзацев.

Для справки. Основная мысль – задача статьи/произведения, а тема – обобщенное название содержания.

С чего начать и как закончить:

1. Прочитайте текст 2 – 3 раза. Делайте пометки, записывайте идеи по ходу чтения. Если пишете из головы, и вам не нужно изучать конкурентные статьи, тогда пропускайте этот шаг.
2. Задайте себе два вопроса: какова его тема, для чего написан материал. Так вы сразу определитесь с главной мыслью.
3. Присмотритесь к каждому абзацу и подумайте, где ключевой момент, в чем его смысл? Часто абзац – это уже законченная мысль, которую можно внести в структуру как подзаголовок. Не останавливайтесь на деталях. Нас интересуют только действие, сюжетный поворот.
4. Оставьте список на несколько минут, отдохните. Перечитайте его. Понимаете ли вы, о чем работа, только взглянув на него? Да – вы все хорошо проработали, нет – надо дорабатывать.
5. Перепишите план в чистовик, используйте по назначению.

Несколько советов на дорожку:

1. Незнакомые слова, понятия, которыми будете пользоваться, выписывайте отдельно. Обязательно уточните их значение.
2. Не повторяйтесь. Если одно и то же слово напрашивается несколько раз, замените его синонимом.
3. Не бойтесь доработок. Если, вернувшись к списку через несколько минут, вы хотите внести правки, то делайте это.
4. План текста для публичного выступления должен быть коротким. Один пункт состоит максимум из 2 – 3 слов.
5. Оформляйте пункты цифрами, а подпункты маркированным списком.

Заведите отдельный блокнотик для планов. Записывайте туда все свои наработки. Это хороший источник вдохновения, перечитывая который, вы будете отслеживать свой прогресс.

Мы окинули взглядом обобщенный способ структурирования статьи. Теперь усложним задачу и разделим план на несколько видов, каждый из которых создается по-особому.

Какие виды планов существуют?

План помогает нам не запутаться, четко сформулировать, изложить свою мысль. Существует множество вариантов. Сейчас мы рассмотрим наиболее известные методы.

Тезисный

Каждый раздел представлен тезисом. Тезис – краткая формулировка основной идеи 1 – 3 абзацев. Отличительная черта: много глаголов. Он состоит из подлежащего, называющего тему, и сказуемого, раскрывающего ее. Без сказуемого теряется основная мысль.

Как найти тезис? Новичкам сложно выделить основное, отбросив детали. Иногда подзаголовок структуры растягивается на 10 – 15 слов, хотя это недопустимо. Задайте вопросы к абзацам. Но помните: ответ должен состоять из 4 – 8 слов и не более.

Для примера я взяла сказку о золотой рыбке А. С. Пушкина:

1. Жил старче небогато со своей старушкой.
2. Старик поймал волшебную рыбку и отпустил ее.
3. Старче рассказал все старухе, она потребовала корыто.
4. Недовольная старуха послала старика за избой.
5. Сварливой старухе недостаточно избушки, она захотела стать царицей.
6. Надоело быть царицей старушке, захотелось ей стать владычицей морской.
7. Рыбка не вынесла алчности старухи и исчезла.
8. Старик и его жена остались с разбитым корытом.

Каждая 1 000 знаков = 1 тезису. Если вы пишете статью на 6 000 символов, вам нужно выделить 6 пунктов. Так вы не переборщите с водой в тексте, материал будет приятно читать.

Вопросительный

Этот вид структуры построен на вопросах к смысловому блоку текста. Лично мне проще именно так прорабатывать статью. Вопросы возникают еще во время изучения материалов, обдумывания темы.

Такой план идеально подходит для информационных статей, мастер-классов, инструкций, анализа.

Как он выглядит, я снова покажу на примере сказки про золотую рыбку:

1. Что сделал старик, когда выловил волшебную рыбку впервые?
2. Как старуха отреагировала на рассказ о золотой рыбке?
3. Что старуха заставляла мужа просить у рыбки?
4. Как рыбка ответила на последнее желание старушки?
5. Что произошло со стариком и его женой в конце?

Задавайте вопрос с помощью слов: как, когда, почему, чей, сколько, кто. Избегайте вопросительной части “ли”.

Назывной

Назывной план состоит из тезисов, выраженных существительными, прилагательными. Глаголы не нужны. Он очень краткий. Максимальный размер одного заглавия 2 – 4 слова.

Вернемся к нашей сказке о золотой рыбке, чтобы увидеть назывной план на практике:

1. Встреча старика и золотой рыбки.
2. Прихоти старухи.
3. Старик и старуха у разбитого корыта.

Вспомнили классику детства? Значит, все верно. Если только одного взгляда на план хватает, чтобы вспомнить содержимое статьи, вы на правильном пути.

Опорный

Опорный план пишется без правил. Это небольшой пересказ статьи, состоящий из главных информативных частей. Он предназначен для личного пользования. Важно, чтобы вам было удобно и понятно работать с ним. Все пункты – опоры, вызывающие яркие, детальные картины, передающие содержание статьи.

Вы можете писать его развернуто или сжато. Все зависит от вашей цели, возможностей, памяти, ассоциаций.

Вот как я вижу правильно написанный опорный план знаменитой сказки:

1. Первая встреча старика и золотой рыбки.
2. Три желания старухи.
3. Отказ рыбки.
4. Разбитое корыто.

Опорную структуру составляют для публичных выступлений, презентаций, новостных статей и кратких обзоров. Чтобы не упустить главную мысль, но и не смотреть постоянно в листок. Указывайте факты, цифры, названия предметов, действующих лиц.

Смешанный

Это микс из разновидностей планов. Ставьте вопросы, выписывайте тезисы – никаких ограничений.

Для наглядности покажу комбинированную структуру сказки о золотой рыбке:

1. Старче попалась волшебная рыбка, которую ему стало жалко. Он ее отпустил.
2. Как повела себя старуха, услышав о необычной рыбке?
3. Три желания старухи.
4. Почему золотая рыбка отказалась выполнять последнее желание?
5. Старик и его жена вернулись к прежней жизни.

Можете им пользоваться для любых целей.

Простой и сложный

Какой план вам нужен: развернутый или простой. Чтобы сделать правильный выбор, подумайте, насколько важно описать детали или можно обойтись назывными предложениями?

Простая структура – это 3 – 5 заголовков без подробностей, состоящих из 2 – 5 слов, а сложная – более 5 заголовков с подзаголовками и важными деталями.

Например, сказку “Колобок” можно представить так:

Простая структура	Сложная структура
Лепка колобка. Колобок встретился с зайцем. Колобок встретился с волком. Колобок столкнулся с медведем. Колобок попался лисе. Лиса съела его.	Появление колобка. Кто испек колобка? Когда ожил колобок? Что сделал оживший колобок? Путешествие колобка. Как ушел колобок от зайца? Встреча волка и колобка. Колобок столкнулся с медведем. Чем закончилась встреча колобка и лисы?

Тренируйтесь писать простой план. Как только у вас начнет получаться, пробуйте сделать развернутый.

Как видите, упрощенный вариант указывает только на ключевые моменты, сложный помогает понять поведение героев, развитие сюжетной линии.

Как жанр статьи влияет на создание структуры?

Перед тем как садиться за план, подумайте: к какому стилю относится ваш текст? Будет это научная работа или горячая новость? В чем же отличие:

1. Научная работа строится так, чтобы пошагово доказать определенную теорию, закономерность. Автор излагает аргументы, в подтверждение приводя документы, ссылаясь на авторитетные источники. Читатель постепенно идет к выводу – основной идеи материала, которая находится в конце.
2. Яркая заметка, новость и обзор пишется в другой последовательности. Первые пункты – важная, привлекающая внимание информация, середина подробно раскрывает изложенное в начале, а конец – обобщение, дополнительные сведения.

Все дело в характере текстов. Научные труды читают вдумчиво, уделяя внимание каждому информационному блоку.

Тексты журналистов, копирайтеров не изучают. Их бегло просматривают за едой, в транспорте. Первые абзацы должны цеплять, вызывать желание дочитать до конца. Те, кто не учитывает разницы в стилях, сильно проигрывают: их работы остаются незамеченными.

Типичные ошибки + примеры

В процессе обучения новички часто совершают одни и те же ошибки. Самообучение опасно тем, что автор не всегда вовремя замечает свои слабые места, привыкает к ним, начиная писать в едином стиле последующие планы. Наставник необходим на этом этапе. Где его найти? Не надо далеко ходить, шерстить интернет, мы уже давно занимаемся обучением копирайтингу и готовы вам помочь.

А пока я познакомлю вас с банальными ошибками, которые делают план нерабочим:

1. Нарушение логической связи, каждый пункт живет отдельной жизнью.
2. Пункты пересекаются между собой, смысловые границы нарушены. Автор не смог разделить текст на ключевые моменты или слишком детально описал содержание.
3. Все пункты указывают на второстепенную информацию. Скорее всего автор не сумел определить идею, тему статьи.
4. Пропущены вступление, заключение.
5. Автор подобрал неправильные слова для названия пунктов. Невозможно понять, о чем идет речь.
6. Длина пункта превышает 9 слов, напоминает абзац.
7. Размер пунктов, вид слишком различаются. Это допустимо только при написании комбинированного плана.

Выпишите список ошибок и повесьте на рабочий стол. Каждый раз, когда садитесь готовить план или проверять его, пройдитесь по списку.

Написали план? Не спешите им пользоваться. Дайте отлежаться ему хотя бы несколько часов, а затем оцените его свежим взглядом.

Давайте представим, как бы выглядел неправильный план статьи “Как научить ребенка говорить?”

1. Когда ребенок учится говорить?
2. Ребенок не говорит.
3. Что нужно говорить малышу?
4. Как научить ребенка говорить быстро и четко?
5. Частые ошибки, которые совершают родители: мало читают ребенку, заставляют учиться, ругают.

Даже простой взгляд на такую структуру вызывает хаос в голове: что, зачем, о чем они вообще.

Какие ошибки здесь допущены:

• Пункт 1 – лишнее. Мы ведь говорим о том, как научить малыша разговаривать, а не когда. Про это лучше написать отдельный текст.
• Пункт 2 – тезисный, а мы оформляем все вопросами. Выглядит аляписто, нелогично.
• Пункт 3 можно сделать подпунктом для удобства восприятия.
• Пункт 5 длинный, однородные члены после запятой надо оформить подпунктами.

А вот исправленная версия:

• Вступление.
• Как научить говорить ребенка быстро и четко:
  • чтение вслух,
  • развивающие скороговорки,
  • артикуляционная гимнастика,
  • много общения,
  • словесные игры.
• Почему ребенок не разговаривает?
• Типичные ошибки родителей:
  • назойливое обучение,
  • недостаток внимания.
• Заключение.

Учитесь писать подобные тексты для биржи статей, чтобы зарабатывать.

План – опора, помогающая собрать мысли в кучку. Когда я начинала на бирже статей, я и понятия не имела, как он упрощает жизнь копирайтера. Практикуйтесь как можно больше: пишите сами, анализируйте чужие работы. Помните, что упорство и опыт – ваше подспорье.

Как узнать длины сторон и углы участка по координатам ЕГРН?

К сожалению, в текущих формах электронных выписок из ЕГРН в разделе координат не указываются длины сторон участка и углы при угловых точках. Поэтому для получения этих параметров нужно воспользоваться геодезическим калькулятором по ссылке https://egrp365.ru/gps-calculator/

Скопируйте координаты из раздела 3.2 выписки (на картинке отмечено желтым цветом), вставьте в поле калькулятора. Найдите в шапке таблицы номер локальной системы координат (на картинке отмечено зеленым цветом). Например, СК-50 для Московской области, или МСК-47 для Ленинградской области.

Выберите эту исходную систему координат и нажмите кнопку «Рассчитать»:

Точки пересчитаются в единую глобальную систему координат GPS (WGS-84), отобразятся на карте в пронумерованном виде. И напротив каждой точки появится расчетное значение угла и длина отрезка. Если местоположение на карте оказалось неправильное, поменяйте зону исходной системы координат (в некоторых регионах бывают несколько зон внутри одной системы координат, например «СК-50 зона 2»).

6.3 Способы и точность определения площадей земельных участков

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра.

В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют следующие способы определения площадей:

• аналитический — площадь- вычисляется по результатам измерений линии на местности, результат нм измерении линий и углов на местно­сти или по их функциям (координатам вершин фигур);

• графический — площадь вычисляется по результатам измерений линий или координат на плане (карте);

• механический — площадь определяется по плану с помощью спе­циальных приборов (планиметров) или приспособлений (палеток). Иногда эти способы применят комбинированно (например, часть линейных величин для вычисления площади определяют по плану, а часть берут из результатов измерений на местности).

Площади можно также определить на ЭВМ по цифровой модели местности по специальной программе.

При аналитическом способе определения площадей применяются формулы геометрии, тригонометрии и аналитической геометрии. При определении площадей небольших участков (для учета площадей, занятых строениями, усадьбами, площадей вспашки, посева) их разбивают на простейшие геометрические фигуры, преиму­щественно треугольники, прямоугольники, реже — трапеции. В этом случае площади участков определяются как суммы площадей отдель­ных фигур, вычисляемых по линейным элементам — высотам и ос­нованиям.

Если по границам участка выполнены геодезические измерения, то площадь всего участка или его части можно вычислить по приведенным применительно к следующим фигурам участков:

1) треугольник. Площадь треугольника определяется по сторонам 1, и 12, углу β2 заключенному между ними, по формуле

Р=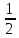 (I112 sin β2); (1)

2) четырехугольник. В зависимости от элементов, известных в четырехугольнике, могут быть использованы различные формулы для расчета, в связи с чем приведем пример, характеризу­ющий это многообразие.

Пусть в четырехугольнике измерены все стороны и один угол при вершине 2. В таком случае площадь тре­угольника 1-2-3 может быть вычислена по формуле (1). При этом полезно вычислить длину 11-3 , используя теорему косинусов:

Площадь треугольника 1-3-4 может быть вычислена по формуле:

где — полупериметр.

Общая площадь четырехугольника

При наличии координат вершин полигона площади треугольни­ка и четырехугольника удобно вычислять соответственно по следу­ющим формулам:

(2)

Если полигон имеет более четырех углов, то площадь его быстрее и с хорошим контролем можно получить по координатам Хi и Уi его вершин или по приращениям координат ΔХ, и ΔУ после увязки по­лигона, например по следующим формулам:

(3)

Координаты вершин полигона для определения площади участка как в государственной, так и в местной системах могут быть полу­чены любым из известных геодезических способов: триангуляцион­ными или линейно-угловыми построениями; проложением полиго­нометрических или теодолитных ходов; угловыми, линейными и полярными засечками; спутниковыми приемниками для определе­ния местоположения и т. д.

Кроме того, когда требуется определить только площадь или гра­ницы участка в его частной системе координат, можно применять так называемый способ изолированных базисов. Суть его заключается в том, что координаты точек объекта определяют засечками с изоли­рованных друг от друга базисов, расположенных в удобных местах внутри (рис.2, а) или вблизи (рис.2, б) участка.

Для приведе­ния результатов измерений в одну систему координат необходимо, чтобы было выполнено условие перекрытия, т. е. со смежных бази­сов должно быть определено несколько (минимум две) общин точек.

Для каждой из п общих точек смежных базисов, например Ь, и Ь2, можно записать два уравнения связи вида:

Рис. 2. Определение координат точек участка с изолированных базисов, находящихся: а — внутри участка; б — вблизи участка

Хj(1)=хj(2)cos φ1,2 -Yj2sin φ1,2 + хс1;

Yj(1)= хj(2)sin φ1,2 + уj2cos φ1,2 + Y с1 (4)

из которых по методу наименьших квадратов определяется угол φ1,2 , разворота систем координат и координаты Хс1и Y с1 начала коорди­нат системы 2 в системе 1. Установив параметры преобразования ко­ординат, в правые части этих формул подставляют координаты и у1(2) остальных (т — п) точек, определенных со второго базиса, пе­реводя их тем самым в первую систему.

Аналогичным образом реша­ется задача для всех точек, определяемых с базисов ЬЗ, Ь4 и т. д.

При графическом способе определения площадей участок на плане делят на простейшие геометрические фигуры.

При разбивке участка на простейшие фигуры можно принять много вариантов, однако точность вычисления площади участка при различных вариантах не будет одинаковой. Площадь треугольника графическим способом вычисляется точнее площадей определяемых

разбивкой на прямоугольники, трапеции и другие фигуры.

Механический способ определения наиболее целесообразно применять для участков с ломаными линиями. Можно оп­ределить площади прямолинейными и криволинейными палетками. При определении площадей по плану графическим или механическим ­ способом (с помощью планиметра и палеток) необходимо учитывать деформацию бумаги (плана). Величина деформации может характеризоваться коэффициентом q, определенным в двух взаимоперпендикулярных направлениях по следующей формуле:

q = , (5)

где Lо — теоретическая длина линии, значащаяся на плане (например, длина стороны квадрата координатной сетки); — результат измерения этой линии по плану.

В настоящее время механические планиметры заменили электронные (цифровые). Представляют интерес цифровые планиметры, например фирмы Topcon, которая предлагает несколько моделей цифровых планиметров, позволяющих проводить измерения площадей по картам или другим материалам с точностью ±0,2 % .

Если для определения площадей используются пункты государственной геодезической сети, то полученные площади чаще всего имеют немного преуменьшенное значение, потому что координаты пунктов относятся не к поверхности Земли, а к поверхности принятого референц – эллипсоида. На больших высотах этой разницей не всегда можно пренебречь.

Переход от площади Р0 на поверхности референц – эллипсоида к площади Р на поверхности Земли на высоте Н может быть выпол­нен по формуле

Р=Ро,(6 ) где R — радиус Земли, равный 6 370 км.

Пользуясь координатами пунктов, планами (картами) в проекции Гаусса-Крюreра, площади участков РпР и размеры получаются всегда больше их горизонтальных проекций, и это увеличение возрастает по мере удаления от осевого меридиана зоны.

Для приведения площади к горизонтальной проекции используют формулу:

2, (7) где Уm — средняя ордината участка (расстояние от осевого меридиа­на зоны до середины участка).

Приведенный способ изолированных базисов свободен от попра­вок за переход от поверхности референц-эллипсоида и проекции Га­усса-Крюгера, так как координаты точек базисов и границ участков определяются в частной системе, на физической поверхности Земли.

Иногда возникает необходимость получения площадей физиче­ской (топографической) поверхности участка РФ, которая тем боль­ше отличается от площади горизонтального проложения участка Р г.п, чем больше угол наклона v или уклон i местности. Для получения площади физической поверхности участка его разбивают на части с одинаковыми скатами, т. е. с равностоящими, и более или менее прямыми горизонталями. На каждой из этих частей в перпендику­лярном направлении к горизонталям определяют угол наклона или уклон и вычисляют площадь РФ на физической поверхности земли по следующим формулам:

Рф=Р г.п ;

Рф=Р г.п (8).

Например, уже при угле наклона v = 2,9 (уклоне i = 0,05) поправка составит 1 : 800, или 12,5 м2 на 1 га.

Требования к точности определения площади земельных участков зависят от многих факторов: хозяйственной значимости (сельскохозяйственные угодья, лесные угодья, городская территория и т. п.), местоположения (центр города, его окраина и т. п.), экологической обстановки (химическая загрязненность земли, атмосферы и т. п.), наличия и ценности недвижимости. Все эти и другие возмож­ные факторы влияют на нормативную стоимость земли, которая в основном и является исходной для расчета требуемой точности оп­ределения площади земельных участков.

Достижение требуемой точности возможно лишь при правильном выборе способа определения площади участка. Очевидно, что наивысшая точность может быть достигнута при аналитическом способе определения площади. При этом способе площадь участка определяется по результатам измерений на местности и погрешность в определении площади зависит от погрешностей этих измерений. Так, погрешность mp площади треугольника и прямоугольника, вычисляемую по измеренным высоте h с погрешностью тh и основанию 1 с погрешностью mi , определяют по формуле (9). При одинаковой относительной погрешности измерения h и l

(9)

(10) Например, при Р =1 га (10 000 м2) и 1/S = 1/2 000 тР=7 м2. Из выражений (23.3) для полигона с п вершинами можно получить фор­мулу погрешности площади вида

(11)

где m — средняя квадратическая погрешность определения коорди­нат х и у точек вершин полигона при условии, что

Di — расстояние от начала координат до i-й точки вершины пол тона (в частном случае — от одной из вершин, принятой за начало координат).

Для прямоугольника со сторонами а и Ь формула (11) примет вид

(12)

а для квадрата со стороной а (13)

Например, если для участка размером 100 х 100 м и площадью 1 га определять координаты со средней квадратической погрешностью 0,02 м, то погрешность площади будет равна 2 м2.

Для погрешности площади участка, определяемой по топографическому плану (карте), с учетом погрешностей измерений на м мости и погрешностей составления топографического плана мо использовать формулу следующего вида:

	Погрешность m, м2, для масштабов
Площадь Р, м2
	3,0	6,0	12,0
	3,6	7,3	14,6
	5,2	10,4	20,8
2 500	7,5	15,0	30,0
10 000	15,0	30,0	60,0

= (14)

где М -знаменатель численного масштаба плана; Р — площадь участка.

В таблице приведены величины средних квадратических погреш­ностей, вычисленных по формуле (14) для различных площадей участков по планам различных масштабов.

Приведенные формулы являются приближенными, так как не учитывают возможных погрешностей исходных данных и зависимо­сти между входящими в них величинами. Однако они вполне доста­точны для предварительных (проектных) расчетов.

5.4 Понятие о геоинформационных системах

Появление современных высокопроизводительных компьютеров с их возможностью переработки, хранения и выдачи огромного количества информации предопределило возникновение нового направления в хозяйственной и управленческой деятельности челове­ка и новой науки — геоинформатики.

Первоначально понятие «геоинформационные системы» (ГИС) расшифровывалось как «географические информационные системы», поскольку оно появилось в недрах географической науки. Сейчас область использования далеко вышла за пределы географии и приставка «гео» свидетельствует лишь о том, что информация свя­зана с Землей и деятельностью человека на ней.

Таким образом, под геоинформационной системой чаще всего понимают компьютерное хранилище знаний о территориальном взаимодействии природы и общества, обеспечивающее сбор, хранение, обработку и визуализацию (зрительное представление) многих видов информации о явлениях в окружающем человека пространстве и во времени. К их числу относится информация из областей гeографии, информатики, гeодезии, картографии, земельного учета, управления, права, экологии и других наук.

Геоинформационные системы подразделяются:

• по территориальному охвату — на общенациональные и региональные;

• по целям использования – многоцелевые, специализированные, информационно-справочные, для нужд планирования, управления и др;

• по тематике — водных ресурсов, использования земель, лесопользования, туризму и др.

Особенно активно развиваются системы, ориентированные на кадастр.

Источниками информации для ГИС в основном являются гeoгpaфические и топографические карты и планы, аэрокосмические материалы, нормативные и правовые документы.

Современные ГИС, как правило, являются цифровыми и создаются с использованием специального программного обеспечения и объема данных, называемого базой данных.

База данных с цифровой карты включает в себя два варианта информации: пространственную, определяющую местоположение объекта, и семантическую (атрибутивную), описывающую свойства объекта.

Многoобразная пространственная информация в ГИС организуется в виде отдельных тематических слоев, отвечающих решению различных задач. Каждый слой может содержать информацию, относящуюся только к одной или нескольким темам. Например, для задач развития гoродской территории набор из отдельных слоев может включать в себя данные: о землевладениях и недвижимости; об объектах транспорта, образования, здравоохранения, культуры; инженерных сетях; рельефе; геодезических сетях и других объектах городского хозяйства.

Для представления карт и планов в компьютере используется пря­моугольная система координат. Каждая точка описывается одной парой координат: Х, У. Пользуясь координатной системой, можно представить точки, линии и полигоны в виде списка координат. При этом для представления земной поверхности на плоскости используются различные картографические проекции, например проекции Гаусса- Крюгера.

Данные с карты, плана вводятся в компьютер путем цифрования. Цифрование может быть выполнено либо путем оцифровки каждой характерной точки объекта, либо путем сканирования всего листа карты электронным сканером. Ввод в базу данных компьютера может также осуществляться с электронных геодезических приборов. Описательные характеристики объектов могут вводиться с клавиатуры компьютера.

Данные аэро- и космических съемок, записанные в цифровом виде, также могут быть введены в компьютер, минуя бумажную стадию.

5.5 . Геоинформационные системы в кадастре

Любой вид кадастра (земельный, градостроительный, водный лесной и др.) является геоинформационной системой, поскольку содержит совокупность достоверных и необходимых сведений о природном, хозяйственном и правовом положении земель и недр на базе картографической информации. Картографическая информации служит и для оценки количества, качества и стоимости земель, регистрации землепользования и землевладения, текущего контроля за землепользованием.

Информационная основа кадастра создается в результате инвентаризации земель и кадастровых съемок. Эти работы могут охватывать как большие территории (город, район, населенный пункт и т. п.), так и небольшие земельные участки.

Чтобы разместить большое количество сведений в единой информационной системе, кадастровая информация делится на элементарные слои, каждый из которых самостоятельно используется для решения конкретной задачи.

Для автоматизированной системы кадастра, основанной на применении ГИС, используются цифровые кадастровые карты, планы. Все объекты, представленные на кадастровой карте, плане, имею пространственную привязку, т. е. их положение определено в том системе координат, которая принята при создании карты. Описательные данные объекта (земельного участка) составляют содержание базы данных информационной системы. Для обозначения и связи объектов этой базы данных используются идентификаторы (кадастровые номера) участков.

Таким образом, цифровая кадастровая карта, представляя собой совокупность метрических (графических) и семантических (описательных) данных, является картографической частью информационной системы кадастра.

Определяя местоположение земельных участков, их границы площади, она используется как инструмент управления земельными ресурсами.

Таким образом, государственный земельный кадастр является геоинформационной системой, обеспечивая сбор, хранение и в земельной информации потребителям.

Способы определения площадей

Размещено на http://www.allbest.ru

Введение

1. Способы определения площадей

1.1 Графический способ определения площадей

1.2 Аналитический способ определения площадей

1.3 Механический способ определения площадей

2. Точность определения площадей

2.1 Исследование ошибок определения площади по результатам измерения на местности

2.2 Исследование ошибок определения площади по плану и влияние деформации бумаги

2.2.1 Ошибки определения площадей графическим способом

2.2.2 Ошибки определения площадей палетками

2.2.3 Деформация бумаги и ее учет при определении площадей

Заключение

Список используемой литературы

Приложение

Введение

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра. В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют следующие способы определения площадей.

Аналитический способ — площадь вычисляется по результатам вычисления координат вершин фигур или по формулам геометрии (при разбивке участка на правильные геометрические фигуры).

Графический способ — площадь вычисляется по карте, используя формулы простых фигур, на которые разбивается участок, или палеткой.

Механический способ — площадь определяется по плану или карте с помощью специального прибора (планиметра).

В данной работе рассматриваются способы определения площадей и анализируется каждый из них на примере выбранного участка, для сравнения точности вычислений.

графический местность площадь

1. Способы определения площадей

При решении многих вопросов, связанных с использованием земельной территории, необходимо знать площади тех или иных участков. Площади участков могут быть определены или по результатам обмера участка в натуре или по планам и картам. Измерение площадей на планах и картах необходимо для решения различных инженерных задач.

Существует три основных способа определения площадей: графический, когда площадь вычисляется по данным, взятым графически с плана или карты; аналитический, когда площадь вычисляют непосредственно по результатам полевых измерений или по их функциям — координатам вершин участка; механический, когда площадь определяется по плану при помощи специальных приборов, называемых планиметрами.

1.1 Графический способ определения площадей

Данный способ заключается в том, что определенный участок на плане разбивают прямыми линиями на ряд простейших геометрических фигур (обычно треугольники, реже — прямоугольники, квадраты или трапеции) и с помощью циркуля-измерителя и масштабной линейки определяют в каждой фигуре размеры тех элементов, которые необходимы для вычисления площади фигуры. Вычислив по известным формулам геометрии площади фигур и взяв их сумму, находят общую площадь участка.

Площади криволинейных контуров удобно определять при помощи палеток. Палетки бывают прямолинейные и криволинейные. К прямолинейным относятся квадратные и параллельные палетки. К криволинейным относятся гиперболические палетки, представляющие систему гиперболических кривых и применяющиеся для определения площадей простейших геометрических фигур. Однако гиперболические палетки применяются редко, так как они не пригодны для быстрого определения площадей с криволинейными контурами.

Палетка (рисунок 1) представляет собой сетку квадратов, нанесенную на восковке или прозрачной целлулоидной пластинке. Стороны квадратов могут быть от 2 до 10 мм. Для определения площади палетку накладывают на контур и считают число квадратов, поместившихся внутри контура. Доли неполных квадратов при этом оценивают на глаз. Зная в масштабе плана площадь одного квадрата, умножением на число квадратов находят общую площадь контура. Квадратная палетка представляет сеть взаимно перпендикулярных линий, проведенных через 1-2мм на прозрачном материале. Для упрощения подсчетов количества клеток проводят утолщенные линии через 0,5см и 1см, чтобы подсчитать клетки группами — в 25 и 100 мм2.

Недостатком квадратной палетки является то, что площади долей квадратиков, рассекаемых контуром, берутся на глаз и то что, подсчет целых квадратиков или их долей сопровождался ошибками.

Рисунок 1

Недостаток квадратной палетки заключается в том, что площади долей клеток оцениваются на глаз, а подсчет целых клеток может сопровождаться ошибками, поэтому не рекомендуется такой палеткой определять площади больше 2 см2на плане.

Отмеченных выше недостатков квадратной палетки не наблюдается при определении площадей параллельной палеткой, представляющей собой лист прозрачного материала, на котором нанесены параллельные линии, в основном через 2 мм одна от другой (рис. 1.2).

Рисунок 1.2

Площадь контура этой палеткой определяют следующим образом. Накладывают ее на контур так, чтобы крайние точки a и b разместились посередине между параллельными линиями палетки. Тогда весь контур окажется расчлененным параллельными линиями на фигуры, близкие к трапециям с одинаковыми высотами, причем отрезки параллельных линий внутри контура являются средними линиями трапеций. На рисунке 1.2 прерывистыми линиями показаны основания этих трапеций. Площадь контура будет равна сумме площадей трапеций:

P = cd h + ef h + mn h + … +kl h (1)

P = h( cd + ef + mn + … + kl), (1.2)

так как высоты в фигурах равны.

Таким образом, чтобы определить площадь контура, следует взять сумму средних линий, то есть сумму отрезков параллельных прямых, проходящих внутри контура, и умножить на расстояние между ними. Параллельная палетка предназначена для определения площадей небольших контуров, при этом не рекомендуется определять ей площади больше 10 см2на плане.

Ошибка определения площади графическим способом равна примерно 1:100 — 1:200 от величины вычисляемой площади. Для повышения точности определения площадей этим способом следует пользоваться планами наиболее крупного масштаба, а также использовать, где это возможно, данные измерений в натуре.

1.2 Аналитический способ определения площадей

Площади вычисляют по результатам измерений линий и углов на местности с применением формул геометрии, тригонометрии и аналитической геометрии.Исходными данными для вычисления площадей данным способом служат координаты вершин многоугольника.Если по результатам измерений на местности определены координаты вершин замкнутого многоугольника, то его площадь может быть определена аналитическим способом. Пусть требуется вычислить площадь полигона 1-2-3-4 (рисунок 2), координаты вершин которого известны: 1 (X1, Y1); 2 (Х2, Y2); 3 (Х3, Y3); 4 (Х4, Y4). Из рисунка 2 видно, что площадь Р данного четырехугольника представляет собой алгебраическую сумму и разность площадей трапеции:

Р = 0,5 . (2)

Раскрыв скобки, выполнив сокращение и приведение подобных членов, получим:

2Р = Х1(Y2 — Y4) + X2(Y3 — Y1) + X3(Y4 — Y2) + X4(Y1 — Y3)

или в общем виде для n-угольника можно записать

2Р= УХi(Yi+1 — Yi-1). (2.1)

Подобным образом из уравнения (1.1) после преобразований можно получить:

2Р= Y1(X4 — X2) + Y3(X1 — X3) + Y3(X2 — X4) + Y4(X3 — X1)

2Р = УYi(Хi-1 — Xi+1). (2.2)

Согласно формулам (2.1) и (2.2) двойная площадь многоугольника равна сумме произведений всех абсцисс на разность ординат последующей и предыдущей вершин, или сумме произведений всех ординат на разность абсцисс предыдущей и последующих вершин.

Следует иметь ввиду, что сумма всех разностей абсцисс (или ординат) от первой до последней точки должна равняться нулю. Это свойство используется для контроля вычисления разностей в формулах (2.1) и (2.2).

Рисунок 2

Погрешность вычислений площадей аналитическим способом не превышает 1:1000 вычисляемой площади.

1.3 Механический способ определения площадей

Определение площадей механическим способом производится при помощи планиметров. Планиметрами называют механические приборы, позволяющие путем обвода плоской фигуры любой формы определить ее площадь. Планиметры бывают различных систем и подразделяются на линейные и полярные. Наибольшее распространение получили полярные планиметры, состоящие из двух рычагов — обводного и полюсного, соединенных шарниром, а также счетного механизма с делениями.

Полюсный рычаг на одном конце имеет груз с короткой иглой (полюсом), а на другом — штифт, который соединяется с обводным рычагом. На конце обводного рычага имеется обводной шпиль (или лупа), которым обводят измеряемую площадь. На обводном рычаге расположен счетный механизм (рисунок 3), состоящий из счетного колеса, разделенного на 100 частей. Ось вращения колеса сопряжена при помощи червячной передачи с циферблатом, разделенным по окружности на 10 частей и снабженным указателем для снятия отсчета.

Рисунок 3 Полярный планиметр: 1 — полюсный рычаг; 2 — обводной рычаг; 3 — обводной шпиль или лупа; 4 — счетное устройство; 5 — счетное колесо; 6 — циферблат; 7 — указатель циферблата; 8 — верньер

Полный отсчет, выраженный в тысячных долях оборота колеса, состоит из четырех цифр, первая из которых берется по указателю циферблата, вторая и третья — по нулевому штриху верньера с ободка колесика. Четвертая отсчитывается по верньеру. Например, отсчет на рисунке 3 составит 3215.

При определении площади фигуры устанавливают планиметр полюсом внутри или вне контура фигуры, а обводной шпиль ставят над какой-либо точкой контура и делают отсчет по счетному механизму U1. После этого тщательно обводят шпилем по ходу часовой стрелки контур фигуры и делают второй отсчет U2. Площадь Рпри полюсе вне фигуры вычисляют по формуле:

Р= С(U2 — U1), (3)

а при полюсе внутри фигуры

Р= С(U2 — U1 + g), (3.1)

Где С- цена деления планиметра; g — постоянное число планиметра.

Перед работой планиметр необходимо поверить и определить его цену деления и постоянное число. При проверке планиметра должны быть проверено выполнение следующих условий:

счетное колесо планиметра должно свободно вращаться на оси без трений и колебаний.

Выполнение этого условия достигается регулировкой подшипников оси колеса при помощи исправительных винтов.

плоскость ободка счетного колеса должна быть перпендикулярна к оси обводного рычага.

Для проверки этого условия обводят одну и ту же фигуру при двух положениях планиметра, когда счетный механизм находится слева и справа от фигуры. Если расхождение между разностями отсчетов в обоих случаях не превышает 2-3 делений планиметра, то условие выполнено. В противном случае площадь следует определять при двух положениях планиметра и брать среднее из результатов.

Цену деления планиметра определяют многократными обводами двух-трех квадратов координатной сетки плана или карты при двух положениях планиметра, помещая полюс вне фигуры. Тогда цена деления будет равна известной площади обводимой фигуры Р, деленной на среднюю разность отсчетов:

С = Р/ (U2 — U1)ср. (3.2)

После определения цены деления планиметра находят его постоянное число. Для этого обводят планиметром большой квадрат координатной сетки с известной площадью при полюсе внутри фигуры. Постоянное число планиметра:

g = P/C — (U2 — U1). (3.3)

При передвижении счетного механизма вдоль обводного рычага изменяется его длина и соответственно изменяется цена деления и постоянное число планиметра. Длина обводного рычага точно фиксируется по шкале с делениями, нанесенными на рычаге.

При определении площадей планиметром необходимо соблюдать следующие правила:

план или карта, по которому определяют площади, должен быть хорошо разглажен и натянут на ровном гладком столе;

положение полюса планиметра выбирают так, чтобы при обводе данной фигуры не образовывались весьма острые или тупые углы между рычагами планиметра и чтобы счетное колесо при этом не сходило с листа бумаги;

обводной шпиль следует вести по контуру плавно, выбирая все изгибы контура. Начальную точку выбирают в таком месте, в котором при обводе счетное колесо почти не вращается;

для контроля и уточнения результатов каждый контур обводят два раза в прямом и обратном направлениях и берут среднее из результатов.

Точность определения площадей планиметром зависит от формы и размеров обводимой фигуры, состояния плана и других причин. Для фигур средней величины (10 — 30 см2) ошибка определения площади планиметром не превышает 1:200 величины площади.

2. Точность определения площадей

2.1 Исследование ошибок определения площади по результатам измерения на местности

В зависимости от хозяйственной значимости участков и массивов, их размеров, конфигурации и вытянутости, наличия планово-топографического материала, топографических условий местности применяются следующие способы определения площадей:

Аналитический — когда площадь вычисляется по результатам измерений линий на местности, по результатам измерений линий и углов на местности или по их функциям (координатам вершин фигур);

Графический — когда площадь вычисляется по результатам измерений линий на плане (карте);

Механический — когда площадь определяется по плану при помощи специальных приборов (планиметров) и приспособлений (палеток) и других.

Иногда эти способы применяются комбинированно, например, часть линейных величин для вычисления площади определяется по плану, а часть берут из результатов измерений на местности. Нередко основная площадь участка, заключенная в теодолитный полигон, определяется аналитическим способом, а площадь, выходящая за пределы полигона и заключенная между линиями полигона и живого урочища, определяется графическим или механическим способом.

Наиболее точным является аналитический способ, поскольку на точность определения площади этим способом влияют только погрешности измерений на местности, в то время как с применением графического и механического способов, помимо погрешностей измерений на местности, влияют погрешности составления плана, определения площадей по плану и деформация бумаги. Однако аналитический способ требует измерения линий и углов по границам участков, больших вычислительных действий, зависящих от количества углов. Целесообразно применять аналитический способ, если число углов по границе участка невелико (не более 10—15).

Наименее точным, но наиболее распространенным является механический способ, так как, пользуясь им, можно быстро и просто определять по плану площадь участка любой формы.

Графический способ выгодно применять в том случае, когда границей участка является ломаная линия с небольшим числом поворотов.

Если площадь фигуры определяется по результатам непосредственных измерений на местности, то можно выполнить предрасчет точности площади по формулам теории ошибок. Ошибки площадей полигонов различной формы вычисляются по таким формулам:

Средняя квадратическая ошибка площади, имеющую форму правильного многоугольника, вычисляется так:

Подставим значение n в эту формулу для таких форм многоугольника:

Треугольник:

mp mi;

Четырехугольник:

mp mi;

Десятиугольник:

mp mi.

Из этого видно, что самой оптимальной формой многоугольника является треугольник.

Средняя квадратическая ошибка площади полигона (участка), которая имеет форму параллелограмма целесообразно находить по такой формуле:

где — средняя квадратическая ошибка единицы веса; l — значения линий; — внутренние углы

По данной формуле можно получить такие формулы ошибок площадей:

Для прямоугольника с соотношением сторон, равным и :

Для ромба :

Для квадрата:

Если полигон имеет изогнутую форму, то формула ошибки для данного случая будет такова:

2.2 Исследование ошибок определения площади по плану и влияние деформации бумаги

2.2.1 Ошибки определения площадей графическим способом

Графический способ вычисления площадей состоит в том, что участок, изображенный на плане, разбивают на простейшие геометрические фигуры (треугольники, прямоугольники, трапеции). В каждой фигуре на плане измеряют высоту и основание, по которым вычисляют площадь, и сумма площадей фигур дает площадь участка.

Если участок разбит на треугольники, то площадь каждого треугольника равна:

P = 0,5lh (4)

Для получения зависимости между относительными средними квадратическими ошибками площади и измерений основания и высоты необходимо прологарифмировать выражение (4):

lnP = lnl + lnh — ln2

Дифференцируя по переменам l и h , получаем:

dP/P = dl/l + dh/h

Относительная средняя квадратическая ошибка площади треугольника равна:

(mp/P)2= (ml/l)2= (mh/h)2

Такую же зависимость можно получить для прямоугольника, параллелограмма, ромба и трапеции, если их площадь вычисляется по основанию и высоте (площадь трапеции по средней линии и высоте).

Ошибки измерения по плану можно считать одинаковыми независимо от длин линий:

(ml/P) = (mh/l) = m

Основание определяется несколько точнее высоты, потому что на определение высоты, помимо ошибки определения на плане, влияет также ошибка проведения основания между вершинами углов, до которого измеряется высота. Однако влияние этой ошибки на ошибку определения высоты невелико, если треугольник равнобедренный. Если же треугольник близок к прямоугольному, то ошибка высоты в 1,2 раза больше ошибки основания. Тогда получаем:

Так как для треугольника lh = 2P , а для остальных фигур lh = P , то получим:

Для треугольника

Для прямоугольника, параллелограмма и трапеции:

Если участок разбивается на треугольники, у которых высоты примерно равны основаниями, то ошибка площади участка вычисляется по формуле:

где m — ошибка определения расстояния по плану.

А для прямоугольника (по форме близкого к квадрату), параллелограмма и трапеции:

Таким образом, площадь треугольника графическим способом вычисляется точнее площадей других фигур, следовательно, разбивкой участка на треугольники вычисляется площадь точнее, чем разбивкой на прямоугольники, трапеции и другие фигуры.

2.2.2 Ошибки определения площадей палетками

Для определения площадей мелких контуров применяют различного рода палетки. Наиболее удобными для пользования и построения являются квадратная и параллельная палетки.

При оценке точности определения площадей палетками принимается во внимание, что ими определяют площади криволинейных контуров, так как площадь участка, ограниченного прямыми линиями, быстрее и точнее можно определить графическим способом.

Палетками определяют площади небольших контуров, не превышающих 10см2 (с.к.о. или m = 0,03).

Таким образом, зависимость ошибки площади от ее величины, определяемой квадратной палеткой, выражается формулой:

Для различных масштабов планов эту формулу можно записать так:

где M — знаменатель численного масштаба плана; P — площадь участка (га).

2.2.3 Деформация бумаги и ее учет при определении площадей

При определении площадей по плану графическим способом необходимо учитывать деформацию бумаги (плана). Величина деформации может характеризоваться коэффициентами, определяемыми в двух взаимно перпендикулярных направлениях, по формуле:

q = (l0 — l) / l0

где l0 — теоретическая длина линии, значащаяся на плане; l — результат измерения этой линии по плану.

Коэффициент деформации бывает 1: 400, 1: 200, 1: 100 и 1: 50. Величина его зависит от сортов бумаги, условий хранения плана, погоды, времени, которое прошло с момента составления плана. Копии с планшетов, отпечатанные на машине, деформируются во время печатания, причем в направлении движения бумага растягивается, а в поперечном направлении сжимается. Через некоторое время деформация бумаги несколько уменьшается, но все же остается значительной.

Особенно сильно деформируется бумага от частого свертывания ее в трубку или складывания вдвое, вчетверо. Если бумага деформируется равномерно, то есть в двух взаимно перпендикулярных направлениях одинаково, то учет деформации не представляет трудности и, наоборот, при неравномерной деформации затрудняется учет, если линия направлена под углом к линиям координатной сетки.

В связи с необходимостью учета деформации бумаги приходится в линии, определенные по плану для вычисления площади, вводить поправки.

Пусть l — результат измерения линии на деформировавшемся плане. Для того чтобы определить соответствующее ей горизонтальное проложение на местности l0, необходимо ввести поправку за деформацию бумаги. Пусть коэффициенты деформации в двух взаимно перпендикулярных направлениях будут различными: qx и qy. Выполнив ряд преобразований, получим:

Если qx и qy или расхождения между ними составляют 20%, то можно принять средний коэффициент деформации q, тогда получим формулу:

где lq — поправка к линии l за деформацию бумаги.

Если поправка в линию меньше точности масштаба (или меньше 0,08мм на плане), то ее можно не вводить в результат измерения линии по плану. По линиям, исправленным за деформацию бумаги, можно вычислять площади фигур. Также, можно определить поправки в площади фигур, полученные по результатам измерений линий на деформировавшемся плане, по таким формулам:

P0= P + P(qx + qy),

где P(qx + qy) — поправка в площадь за деформацию бумаги.

Если коэффициенты равны qx = qy = q или вычислен средний коэффициент:

q = 0,5(qx + qy),

P0= P + 2Pq.

При определении площадей графическим способом, когда участок разбивается на простейшие геометрические фигуры, не целесообразно вводить поправку в площадь каждой из этих фигур, а необходимо исправить общую площадь участка за деформацию бумаги.

Заключение

В данной работе я рассмотрела способы определения площадей земельных участков: графический, аналитический и механический. Определила с их помощью площадь выбранного участка. Оказалось, что самым точным является аналитический способ, самым же неточным графический. Аналитический способ более трудоемкий, по сравнению с графическим и механическим.

Список используемой литературы

1. И.Ф. Куштин, В. И. Куштин. Инженерная геодезия. Ростов-на-Дону: Изд. ФЕНИКС, 2002. — 416 с;

2. М. И. Киселев, Д. Ш. Михелев. Инженерная геодезия. М.: Изд. «Академия», 2007. — 480 с;

3. А. В. Маслов, А. В. Гордеев, Ю. Г. Батраков. Геодезия. М.: КолосС, 2006. — 599 с.

4. А.В. Никитин. Определение площадей земельных участков: Учеб. пособие — Хабаровск: Изд-во ДВГУПС, 2003. — 60 с.

Приложение 1

Определение площади участка графическим способом

Площадь участка определяем при помощи палетки, на которой разбита сетка квадратов со стороной 2мм. Мы прикладываем палетку таким образом, чтобы весь участок был внутри квадрата. Затем производим подсчет сначала целых квадратов внутри участка, а затем складывают неполные квадраты, оценивая их в частях полных, в результате площадь равна произведению площади одного квадрата на число всех квадратов.

Где n — это число всех квадратов

Определение площади участка механическим способом

Определяем цену деления планиметра путем обвода несколько раз границы квадрата со стороной 10 см. При этом снимаем отсчет с планиметра и записываем его. По данной формуле определяется цена деления планиметра:

Где S- это площадь квадрата, — это разность отсчетов по планиметру.

Таблица 1

Отсчет по планиметру ni	Цена деления, сi
					0,093
					0,093
					0,093
					0,093

сср= 0,093

Площадь определяется по формуле:

n2 = 7146, n1 = 6456

Определение площади участка аналитическим способом

Таблица 2 Координаты вершин земельного участка

№ точки	X, м	Y, м	№ точки	X, м	Y, м

Площадь вычисляем по формулам (2.2):

Единицы измерения площади земельных участков

Перед вычислением площади участка полезно узнать…

Принятая в России система измерения площадей земельных участков установлена Постановлением Правительства РФ «Положение о единицах величин, допускаемых к применению в Российской Федерации» № 879 от 31.09.2009 г.

В соответствии с этим постановлением, допускаются к применению единицы, основанные на Международной системе величин (СИ):

• основные единицы СИ
• производные единицы СИ
• отдельные внесистемные единицы величин

Кроме того, предписание об обязательном использовании единиц СИ изложено в действующем в России межгосударственным стандарте ГОСТ 8.417-2002, в котором перечислены единицы физических величин, разрешённые к применению, приведены их международные и русские обозначения и установлены правила их использования.

Международная система единиц СИ — самая используемая система единиц в мире как в повседневной жизни, так и в науке и технике. В настоящее время СИ принята в качестве основной системы единиц большинством стран мира и почти всегда используется в области техники, даже в тех странах, в которых в повседневной жизни используются традиционные единицы.

СИ определяет 7 основных единиц физических величин и производные единицы (сокращённо — единицы СИ или единицы), а также набор приставок.

СИ также устанавливает стандартные сокращённые обозначения единиц и правила записи производных единиц.

Основные единицы СИ

• килограмм (кг, kg) — единица массы
• метр (м, m) — единица длины
• секунда (с, s) — единица времени
• ампер (А, А)- единица силы электрического тока
• моль (моль, mol)- единица количества вещества
• кандела (кд, cd)- единица силы света
• кельвин (К, К)- это 1/273,16 часть термодинамической температуры тройной точки воды:
  1. градус Цельсия (°C) — широко распространённая единица измерения температуры, применяется в СИ наряду с кельвином

Пересчёт в градусы Цельсия:

tC = tK — 273,15 (температура тройной точки воды +0,01 °C).

В рамках СИ считается, что основные единицы имеют независимую размерность, то есть ни одна из них не может быть получена из других.

Производные единицы получаются из основных с помощью алгебраических действий, таких как умножение и деление. Некоторым из производных единиц в СИ присвоены собственные наименования, например, единице радиан.

Приставки CИ нужно использовать перед наименованиями единиц. Они означают, что единицу нужно умножить или разделить на определённое целое число, являющееся степенью числа 10, число раз.

Десятичные приставки служат для сокращения количества нулей в численных значениях физических величин.

Например:

• приставка «кило» означает умножение исходной единицы метр на 1000 (километр = 1000 метров)
• дольная приставка «милли» означает умножение исходной единицы метр на 10-3 (миллиметр = 0.001 метров)
• дольная приставка «деци» означает умножение исходной единицы метр на 10-1 (дециметр = 0.1 метров)

Единицы измерения площади

Касательно единиц измерения площади, являющихся производными от основной единицы длины метр, перечень наименований выглядит так:

• длина
  1. единица измерения — метр
  2. обозначение (русское) — м
  3. обозначение (международное) — m
• площадь
  1. единица измерения — квадратный метр
  2. обозначение (русское) — м2
  3. обозначение (международное) — m2

Пояснение

Метр — длина пути, проходимого светом в вакууме за интервал времени
1/299792458 секунды (XVII Генеральная конференция по мерам и весам (ГКМВ), 1983 год, Резолюция 1).

XXV ГКМВ, состоявшаяся в 2014 году, приняла решение продолжить работу по подготовке новой ревизии СИ, включающей переопределение метра, и предварительно наметила закончить эту работу к 2018 году с тем, чтобы заменить существующую СИ обновлённым вариантом на XXVI ГКМВ в том же году.

Распространённая в России система измерения площадей земельных участков (внесистемная по отношению к СИ)

• 1 сотка = 10 м х 10 м = 10м х 10 м = 100 м2
• 1 гектар = 1 га = 100 м х 100 м = 10000 м2 = 100 соток
• 1 квадратный километр = 1 км2 = 1000 м х 1000 м = 1 млн. км2 = 100 га = 10 000 соток

Обратные единицы

• 1 м2 = 0,01 сотки = 0,0001 га = 0,000001 км2
• 1 сотка = 0,01 га = 0,0001 км2

Таблица перевода единиц измерения площади

Единицы измерения площади	1 кв. км.	1 Гектар	1 Акр	1 Сотка	1 кв.м.
1 км2	1	100	247.1	10.000	1.000.000
1 гектар	0.01	1	2.47	100	10.000
1 акр	0.004	0.405	1	40.47	4046.9
1 сотка	0.0001	0.01	0.025	1	100
1 м2	0.000001	0.0001	0.00025	0.01	1

• Гектар

единица площади в метрической системе мер, применяемая для измерений земельных участков.

Сокращённое обозначение:

• русское — га
• международное — ha

1 га равен площади квадрата со стороной 100 м

Наименование «гектар» образовано добавлением приставки «гекто…» к наименованию единицы площади «ар»:

1 га = 100 ар = 100 м х 100 м = 10 000 м2

• Ар — единица площади в метрической системе мер, равна площади квадрата со стороной в 10 м:
  1. 1 ар = 10 м х 10 м = 100 м2
  2. 1 десятина = 1,09254 га

• Акр

земельная мера, применяемая в ряде стран, использующих английскую систему мер (Великобритания, США, Канада, Австралия и др.).

1 акр = 4840 кв.ярдов = 4046,86 м2

Наиболее употребительная в практике земельная мера гектар — сокращенное обозначение га:

1 га = 100 ар = 10 000 м2

В России гектар является основной единицей измерения площади земли, особенно сельскохозяйственной.

На территории России единица «гектар» была введена в практику после Октябрьской революции, вместо десятины.

Старинные русские единицы измерения площадей

• 1 кв. верста = 250 000 кв. саженей = 1,1381 км2
• 1 десятина = 2400 кв. саженей = 10 925,4 м2 = 1,0925 га
• 1 четь = 1/2 десятины = 1200 кв. саженей = 5462,7 м² = 0,54627 га
• 1 осьминник = 1/8 десятины = 300 кв.саженей = 1365,675 м2 ≈ 0,137 га

Площадь земельных участков для ИЖС, ЛПХ обычно указывают в сотках

Одна сотка — это площадь участка размером 10 х 10 метров, которая составляет 100 квадратных метров, и поэтому называется соткой.

Вот несколько характерных примеров размеров, которые может иметь земельный участок площадью 15 соток:

ширина 15 м, длина 100 м	S = 1500 м2	S = 15 соток
ширина 20 м, длина 75 м	S = 1500 м2	S = 15 соток
ширина 25 м, длина 60 м	S = 1500 м2	S = 15 соток
ширина 30 м, длина 50 м	S = 1500 м2	S = 15 соток

В будущем, если вы вдруг забудете, как найти площадь прямоугольного земельного участка, вспоминайте очень старый анекдот. «Дедушка спрашивает у пятиклассника: «Как найти площадь Ленина?» А тот отвечает: «Нужно ширину Ленина умножить на длину Ленина» :)))

Полезно ознакомиться и с этим

• С используемыми в России масштабами топографических карт можно .

• Узнать о новом Классификаторе ВРИ – 2019 можно

• С 1 января 2018 года в кадастровом паспорте должны быть зафиксированы точные границы участка, поскольку купить, продать, заложить или подарить землю без точного описания границ будет попросту невозможно. Так регламентировано поправками к Земельному кодексу. А тотальная ревизия границ по инициативе муниципалитетов началась с 1 июня 2015 г.

• С 1 марта 2015 года вступил в силу новый Федеральный закон «О внесении изменений в Земельный кодекс РФ и отдельные законодательные акты РФ» (N 171-ФЗ от 23.06.2014 в соответствии с которым, частности, упрощена процедура выкупа земельных участков у муниципалитетов. Ознакомиться с основными положениями закона можно .

• В отношении регистрации домов, бань, гаражей и других построек на земельных участках, находящихся в собственности граждан, улучшит ситуацию новая дачная амнистия

Как посчитать сотки земли и измерить площадь участка? на сайте Недвио

Сотки и гектары — это общепринятые единицы площади земельных участков. Но как понять действительные размеры участка? Если это прямоугольная территория, с ровными границами — то здесь достаточно элементарных знаний математики, а если нет — здесь без сложных расчетов и калькулятора не обойтись.

В этой статье мы рассмотрим основные методики расчета площади участков и их особенности применения.

Чему равна сотка? Сколько квадратных метров в сотке?

Сотка земли — это участок площадью 100 кв. м. (сто квадратных метров).

Почему эта единица измерения получила такое название? Есть несколько версий: кто-то считает, что «сотками» стали называть участки земли из-за их площади (100 м2 — сто метров — сотка), кто-то полагает, что термин произошел, как сотая часть гектара (1 га = 10.000 кв. м / 100). Есть и второе название этой меры измерения площади участков — «ар». Но оно сегодня используется крайне редко.

Мера деления участков на сотки прижилась в большинстве стран. Сотками удобно считать площадь не только земель, но и сада, огорода, дачного участка, при определении территорий для продажи и строительства.

Интересно отметить, что далеко не все страны измеряют площадь участков в сотках. В Англии и США, например, земля измеряется в акрах и квадратных ярдах, а для обозначения расстояния вместо метров используют футы и мили.

В нашей стране, термины «сотка» и «гектар» вошли в обиход только после 1917 года. До этого использовали десятины, версты и другие величины измерения.

Сегодня, в сотках меряют обычно небольшие участки. Если идет расчет размеров участков средней площади, где стороны имеют расстояния более 100 кв. метров, обычно используют единицы в 1 га (гектар). Для того, чтобы посчитать размеры больших участков принято использовать единицы площади в 1 квадратный километр (1 кв. км). Так, территории стран, областей, крупных городов обычно рассчитывают именно в км2.

Как рассчитать сколько соток на участке?

Площадь небольшой территории (как например садового участка) вполне можно рассчитать самостоятельно. Для этого чаще всего используют следующий метод:

1. по углам участка ставят палки-колышки;
2. затем двумя обычными рулетками измеряют расстояние в четыре стороны;
3. полученные данные фиксируются и записываются на бумагу.

Что делать дальше? Возьмем пример: Допустим, мы померяли рулеткой расстояние от колышка к колышку и получили 50 метров по одной стороне, и 35 м — по второй. Согласно правилам геометрии площадь прямоугольной фигуры равна произведению сумм двух смежных сторон. Очевидно, что нам нужно умножить 50 на 35, и мы получим площадь — 1750 кв. м.

После того, как мы определили площадь в квадратных метрах, нам нужно перевести эти значения в сотки. Как мы уже говорили, сотка — это 100 кв. м земли. Поэтому, чтобы узнать площадь нашего участка в сотках нужно разделить 1750 / 100. То есть наш участок имеет размер 17,5 соток.

Эти же правила справедливы и в обратную сторону. Так, к примеру, если вы видите объявление о продаже земельного участка размером в 9 соток — это значит, что его площадь равна 900 квадратных метров (9 * 100 = 900).

А вот с длиной сторон участков уже посложнее. 900 кв. м. — могут быть как форме квадрата (30 х 30 м), так могут быть и в форме прямоугольника (например, 20 х 45 м или 25 х 36 м), а могут и вовсе иметь разную длину сторон.

Формулы расчета площади участков. Примеры

Приведем для понимания несколько примеров расчетов:

• 10 соток нужно перевести в квадратные метры. Тогда 10 * 100 = 1000 кв. м;
• Какова площадь территории прямоугольной формы со сторонами 25 и 30 м. Считаем: 25 * 30 / 100 = 7,5 сот.;
• Каковы размеры сторон участка в 25 соток. 25 сот. — это 2500 кв. м. Вычисляем корень квадратный из 2500, получаем 50 м;
• Какова площадь участка со сторонами 20 и 10 м. Считаем: 20 × 10 = 200 кв. м. или 2 сотки.

Наиболее сложные случаи возникают при определении размеров земельных участков неправильной формы. Для этого нужно знать размеры каждой из сторон и лучше использовать специальный калькулятор:

Как применять эти данные?

Допустим, вы планируете построить дом площадью 100 квадратных метров на участке в 8 соток. Соответственно 100 делим на 1 и получаем, то дом займет территорию в 1 сотку. Остальные 7 соток мы можем использовать по своему усмотрению: разбить огород, построить гараж, бани, теплицы и т. д.

Вы можете нарисовать план участка на бумаге, определить, где находится дом, сколько места он занимает, а также расположение других строений и насаждений.

Измерение площади участка шагами

Если при осмотре интересующей территории, у вас нет с собой измерительных приборов, и даже рулетки, можно посчитать площадь участка «на глаз». Как вариант — способ посчитать размер участка шагами.

Общеизвестно, что размер шага обычного человека — 0,7 м. Таким образом для того чтобы рассчитать сто квадратных метров, вы делаете 12-14 шагов в одну сторону, затем под прямым углом делаете такое же количество шагов в другую сторону. Квадрат в 12-14 шагов — это и есть сотка земли.

Как измерить площадь участка палкой?

Еще один способ как можно измерить площадь — соорудить палку длиной в 1 метр (или два) и делать замеры с помощью нее.

Наиболее точной длину палки можно сделать при помощи роста тела или же какого-либо предмета, размер которого известен. Это может быть тротуарная плитка (обычно 30 см) , столбик ограждения или же можно измерить растяжкой большого и указательного пальца (приблизительно 20 см) .

Как рассчитать сотку земли при помощи палки? Очень просто. Отмерьте ей 10 раз обе стороны участка и у вас получится сто квадратных метров.

Есть и более продвинутый способ применения этого способа, когда из трех палок делается тренога или, как еще называют, «сажень». По опыту скажем, что измерять участок сажнем выходит намного быстрее.